Using R and lme/lmer to fit different two- and three-level longitudinal models

April 21, 2015

I often get asked how to fit different multilevel models (or individual growth models, hierarchical linear models or linear mixed-models, etc.) in R. In this guide I have compiled some of the more common and/or useful models (at least common in clinical psychology), and how to fit them using nlme::lme() and lme4::lmer(). I will cover the common two-level random intercept-slope model, and three-level models when subjects are clustered due to some higher level grouping (such as therapists), partially nested models were there are clustering in one group but not the other, and different level 1 residual covariances (such as AR(1)). The point of this post is to show how to fit these longitudinal models in R, not to cover the statistical theory behind them, or how to interpret them.

Data format

In all examples I assume this data structure.

subjects	tx	therapist	time	y
1	0	1	0	10
1	0	1	1	12
1	0	1	2	14
2	0	1	0	4
2	0	1	1	14
2	0	1	2	13
3	0	2	0	12
3	0	2	1	15
3	0	2	2	16
4	0	2	0	17
4	0	2	1	13
4	0	2	2	12
5	0	3	0	15
5	0	3	1	13
…	…	…	…	…

Where subjects is each subject’s id, tx represent treatment allocation and is coded 0 or 1, therapist is the refers to either clustering due to therapists, or for instance a participant’s group in group therapies. Y is the outcome variable.

Power analysis, and simulating these models

Most of the designs covered in this post are supported by my R package powerlmm, (http://cran.r-project.org/package=powerlmm). It can be used to calculate power for these models, or to simulate them to investigate model misspecification. I will soon integrate the package into this post, in order to create example data sets. For now, see the package’s vignettes for tutorials.

Longitudinal two-level model

We will begin with the two-level model, where we have repeated measures on individuals in different treatment groups. Two-level multilevel model in R. By Kristoffer Magnusson

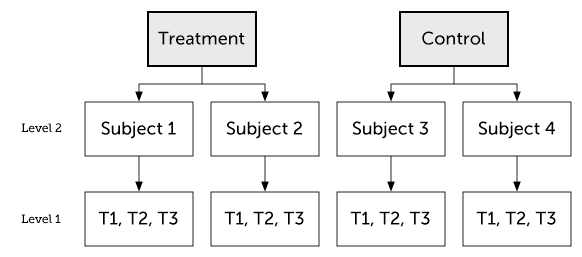
Unconditional model

Model formulation

Level 1 Y_{i j} Level 2 β_{0 j} = β_{0 j} + R_{i j} = γ_{00} + U_{0 j}

with,

U_{0 j} \sim N (0, τ_{00}^{2}),

and

R_{i j} \sim N (0, σ^{2})

To fit this model we run

Unconditional growth model

Model formulation

Level 1 Y_{i j} Level 2 β_{0 j} β_{1 j} = β_{0 j} + β_{1 j} t_{i j} + R_{i j} = γ_{00} + U_{0 j} = γ_{10} + U_{1 j}

with,

(U_{0 j} U_{1 j}) \sim N (00, τ_{00}^{2} τ_{01} τ_{01} τ_{10}^{2}),

and

R_{i j} \sim N (0, σ^{2})

To fit this model we run

Conditional growth model

Model formulation

Level 1 Y_{i j} Level 2 β_{0 j} β_{1 j} = β_{0 j} + β_{1 j} t_{i j} + R_{i j} = γ_{00} + γ_{01} T X_{j} + U_{0 j} = γ_{10} + γ_{11} T X_{j} + U_{1 j}

with,

(U_{0 j} U_{1 j}) \sim N (00, τ_{00}^{2} τ_{01} τ_{01} τ_{10}^{2}),

and

R_{i j} \sim N (0, σ^{2})

To fit this model we run

Conditional growth model: dropping random slope

Model formulation

Level 1 Y_{i j} Level 2 β_{0 j} β_{1 j} = β_{0 j} + β_{1 j} t_{i j} + R_{i j} = γ_{00} + γ_{01} T X_{j} + U_{0 j} = γ_{10} + γ_{11} T X_{j}

with,

U_{0 j} \sim N (0, τ_{00}^{2})

and

R_{i j} \sim N (0, σ^{2})

To fit this model we run

Conditional growth model: dropping random intercept

Model formulation

Level 1 Y_{i j} Level 2 β_{0 j} β_{1 j} = β_{0 j} + β_{1 j} t + R_{i j} = γ_{00} + γ_{01} T X_{j} = γ_{10} + γ_{11} T X_{j} + U_{1 j}

with,

U_{1 j} \sim N (0, τ_{10}^{2})

and

R_{i j} \sim N (0, σ^{2})

To fit this model we run

Conditional growth model: dropping intercept-slope covariance

Model formulation

Level 1 Y_{i j} Level 2 β_{0 j} β_{1 j} = β_{0 j} + β_{1 j} t + R_{i j} = γ_{00} + γ_{01} T X_{j} + U_{0 j} = γ_{10} + γ_{11} T X_{j} + U_{1 j}

with,

(U_{0 j} U_{1 j}) \sim N (00, τ_{00}^{2} 0 0 τ_{10}^{2}),

and

R_{i j} \sim N (0, σ^{2})

To fit this model we run

Three-level models

Here I will cover some different three-level models. In my examples clustering at the highest level is due to therapists. But the examples generalize to other forms of clustering as well, such as group therapy or clustering due to health-care provider. Three-level multilevel model in r. By Kristoffer Magnusson

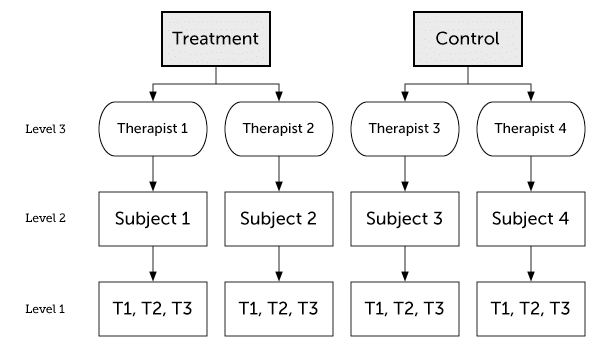
Conditional three-level growth model

We will jump straight to the conditional three-level growth model, with the following model formulation:

Level 1 Y_{i j k} Level 2 β_{0 j k} β_{1 j k} Level 3 γ_{00 k} γ_{10 k} = β_{0 j k} + β_{1 j k} t_{i j k} + R_{i j k} = γ_{00 k} + U_{0 j k} = γ_{10 k} + U_{1 j k} = δ_{000} + δ_{001} T X_{k} + V_{0 k} = δ_{100} + δ_{101} T X_{k} + V_{1 k}

with,

(U_{0 j} U_{1 j}) \sim N (00, τ_{00}^{2} τ_{01} τ_{01} τ_{10}^{2}),

and,

(V_{0 k} V_{1 k}) \sim N (00, φ_{00}^{2} φ_{01} φ_{01} φ_{10}^{2}),

and

R_{i j k} \sim N (0, σ^{2})

To fit this model we use therapist/subjects, which specifies nesting. This formula expands to a main effect of therapist and a interaction between therapist and subjects (which is the subject level effect).

Subject level randomization (therapist crossed effect)

In the previous example therapists only provided one type of treatment (nested design). Sometimes therapists will be a crossed effect, i.e. in a parallel group design they will deliver both treatments. If it’s a randomized trial then in this design we have subject level randomization, whereas in the previous example randomization was at the therapist level.

Three-level multilevel model in r: subject-level randomization. By Kristoffer Magnusson

Level 1 Y_{i j k} Level 2 β_{0 j k} β_{1 j k} Level 3 γ_{00 k} γ_{10 k} γ_{01 k} γ_{11 k} = β_{0 j k} + β_{1 j k} t_{i j k} + R_{i j k} = γ_{00 k} + γ_{01 k} T X_{j k} + U_{0 j k} = γ_{10 k} + γ_{11 k} T X_{j k} + U_{1 j k} = δ_{000} + V_{0 k} = δ_{100} + V_{1 k} = δ_{010} + V_{2 k} = δ_{110} + V_{3 k}

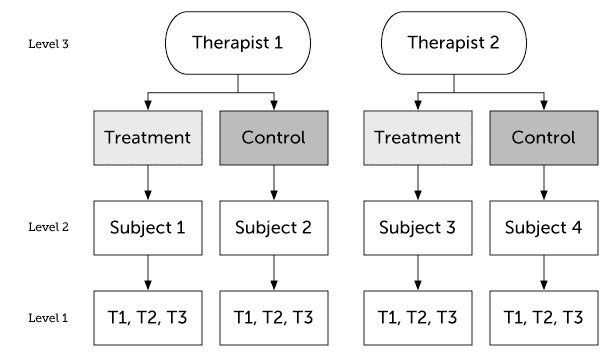
with,

(U_{0 j} U_{1 j}) \sim N (00, τ_{00}^{2} τ_{01} τ_{01} τ_{10}^{2}),

and,

⎝ ⎜ ⎜ ⎜ ⎛ V_{0 k} V_{1 k} V_{2 k} V_{3 k} ⎠ ⎟ ⎟ ⎟ ⎞ \sim N ⎝ ⎜ ⎜ ⎜ ⎛ 0000, φ_{00}^{2} 000 0 φ_{10}^{2} 00 00 φ_{20}^{2} 0 000 φ_{30}^{2} ⎠ ⎟ ⎟ ⎟ ⎞,

and

R_{i j k} \sim N (0, σ^{2})

In this model we estimate no covariances at level 3. However, at the therapist level we have random effects for time, treatment and time treatment*. I fit this saturated model because you can easily delete a random effect in the expanded lmer syntax below.

Different level 3 variance-covariance matrix

We might hypothesize that therapists that are allocated participants that report worse symptoms at treatment start have better outcomes (more room for improvement). To allow for separate covariances in each treatment group we update the variance-covariance matrix at level 3

⎝ ⎜ ⎜ ⎜ ⎛ V_{0 k} V_{1 k} V_{2 k} V_{3 k} ⎠ ⎟ ⎟ ⎟ ⎞ \sim N ⎝ ⎜ ⎜ ⎜ ⎛ 0000, φ_{00}^{2} φ_{01} 00 φ_{01} φ_{10}^{2} 00 00 φ_{20}^{2} φ_{23} 00 φ_{23} φ_{30}^{2} ⎠ ⎟ ⎟ ⎟ ⎞

To fit this model we run

Of course, we could also estimate all six covariances at level 3. For instance, we could look at if therapists who are more successful with Treatment A are also more successful with Treatment B, i.e. $c o v (V_{2 k}, V_{3 k}) = φ_{23}$ , and so forth. The full unstructured level 3 variance-covariance matrix we will estimate is thus

⎝ ⎜ ⎜ ⎜ ⎛ V_{0 k} V_{1 k} V_{2 k} V_{3 k} ⎠ ⎟ ⎟ ⎟ ⎞ \sim N ⎝ ⎜ ⎜ ⎜ ⎛ 0000, φ_{00}^{2} φ_{01} φ_{02} φ_{03} φ_{01} φ_{10}^{2} φ_{12} φ_{13} φ_{02} φ_{12} φ_{20}^{2} φ_{23} φ_{03} φ_{13} φ_{23} φ_{30}^{2} ⎠ ⎟ ⎟ ⎟ ⎞

Which we fit by running

Partially nested models

Partially nesting occurs when we have nesting in one group but not the other. For instance, we might compare a treatment group to a wait-list condition. Subjects in the wait-list will not be nested, but subjects in treatment group will be nested within therapists.

Partially-nested growth model in R. By Kristoffer Magnusson

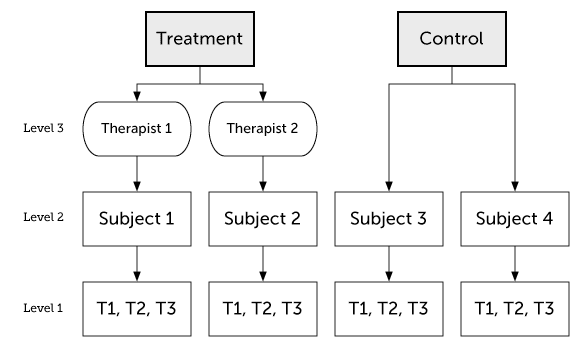
We can write this model like this

Level 1 Y_{i j k} Level 2 β_{0 j k} β_{1 j k} Level 3 γ_{01 k} γ_{11 k} = β_{0 j k} + β_{1 j k} t_{i j k} + R_{i j k} = γ_{00} + γ_{01 k} T X_{j k} + U_{0 j k} = γ_{10} + γ_{11 k} T X_{j k} + U_{1 j k} = δ_{010} + V_{0 k} = δ_{110} + V_{1 k}

with,

(U_{0 j} U_{1 j}) \sim N (00, τ_{00}^{2} 0 0 τ_{10}^{2}),

and,

(V_{0 k} V_{1 k}) \sim N (00, φ_{00}^{2} 0 0 φ_{10}^{2}),

and

R_{i j k} \sim N (0, σ^{2})

More on level 1 specification

Heteroscedasticity at Level 1

Only lme allows modeling heteroscedastic residual variance at level 1. If we wanted to extend our two level model and allow for different level 1 residual variance in the treatment groups, we’d get

(R_{i j} ∣ TX = 0) (R_{i j} ∣ TX = 1) \sim N (0, σ_{0}^{2}) \sim N (0, σ_{1}^{2})

If we wanted to extend our two-level model with this level 1 structure we’d run

More grouping

We could also add another grouping factor such as time, and fit a model with heteroscedastic level 1 residuals for each time point in each treatment group. For instance, for i = 0, 1, 2 we get

(R_{i j} ∣ TX = 0) \sim N ⎝ ⎛ 000, σ_{00}^{2} 00 0 σ_{01}^{2} 0 00 σ_{02}^{2} ⎠ ⎞

(R_{i j} ∣ TX = 1) \sim N ⎝ ⎛ 000, σ_{10}^{2} 00 0 σ_{11}^{2} 0 00 σ_{12}^{2} ⎠ ⎞

which we’d fit by running

First-order Autoregressive AR(1) residuals

For $T = 1, 2, 3, . . ., N_{1}$ time points we get the level 1 variance-covariance matrix

Σ = σ^{2} ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 ρ ρ^{2} ⋮ ρ^{T - 1} ρ 1 ρ ⋮ ρ^{T - 2} ρ^{2} ρ 1 ⋮ ρ^{T - 3} \dots \dots \dots ⋱ \dots ρ^{T - 1} ρ^{T - 2} ρ^{T - 3} ⋮ 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞

we leads to

R_{i j} \sim N (0, Σ)

To fit this level 1 residual structure we use the correlation argument.

Heterogenous AR(1)

We can also extend the level 1 variance-covariance matrix from above, to allow for different residuals at each time point.

Σ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ σ_{0}^{2} σ_{1} σ_{0} ρ σ_{2} σ_{0} ρ^{2} ⋮ σ_{T} σ_{0} ρ^{T - 1} σ_{0} σ_{1} ρ σ_{1}^{2} σ_{2} σ_{1} ρ ⋮ σ_{T} σ_{1} ρ^{T - 2} σ_{0} σ_{2} ρ^{2} σ_{1} σ_{2} ρ σ_{2}^{2} ⋮ σ_{T} σ_{2} ρ^{T - 2} \dots \dots \dots ⋱ \dots σ_{0} σ_{i} ρ^{T - 1} σ_{1} σ_{i} ρ^{T - 2} σ_{2} σ_{i} ρ^{T - 3} ⋮ σ_{T}^{2} ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞

and we have that

R_{i j} \sim N (0, Σ)

To fit this level 1 model we simply use both the correlation and the weights argument.

More level 1 variance-covariances matrices

Se ?corClasses for the different types of residual variance-covariances matrices lme can estimate.

Changing the functional form of time

All of the examples above assume linear change. Here I will cover some examples of how to model nonlinear change at level 1. The examples will be based on the two-level model, but you could easily be combined them with the three-level models outlined above.

Quadratic trend

Level 1 Y_{i j} Level 2 β_{0 j} β_{1 j} β_{2 j} = β_{0 j} + β_{1 j} t_{1 i j} + β_{2 j} t_{1 i j}^{2} + R_{i j} = γ_{00} + γ_{01} T X_{j} + U_{0 j} = γ_{10} + γ_{11} T X_{j} + U_{1 j} = γ_{20} + γ_{21} T X_{j} + U_{2 j}

with,

⎝ ⎛ U_{0 j} U_{1 j} U_{2 j} ⎠ ⎞ \sim N ⎝ ⎛ 000, τ_{00}^{2} τ_{01} τ_{02} τ_{01} τ_{10}^{2} τ_{12} τ_{02} τ_{12} τ_{20}^{2} ⎠ ⎞,

and

R_{i j} \sim N (0, σ^{2})

Orthogonal polynomials

If you’d like to fit orthogonal polynomials you can use the poly() function with raw = FALSE (which is the default).

Piecewise growth curve

Segmenting the time trend into different pieces has got more to do with simple dummy coding of regression variables, than any specifics of lme or lmer. However, I will cover some common scenarios anyway.

To fit a piecewise growth model we simply replace time with two dummy variables time1 and time2, that represent the different time periods. A common scenario is that the first piece represents the acute treatment phase, and piece 2 represent the follow-up phase.

Coding scheme 1: separate slopes

Time	0	1	2	3	4	5
Time 1	0	1	2	2	2	2
Time 2	0	0	0	1	2	3

Coding scheme 2: incremental/decremental slope

Time	0	1	2	3	4	5
Time 1	0	1	2	3	4	5
Time 2	0	0	0	1	2	3

These two coding schemes only differ in the interpretation of the regression coefficients. In scheme 1 the two slope coefficients represent the actual slope in the respective time period. Whereas in scheme 2 the coefficient for time 2 represents the deviation from the slope in period 1, i.e. if the estimate is 0 then the rate of change is the same in both periods.

Piecewise growth model in R. By Kristoffer Magnusson

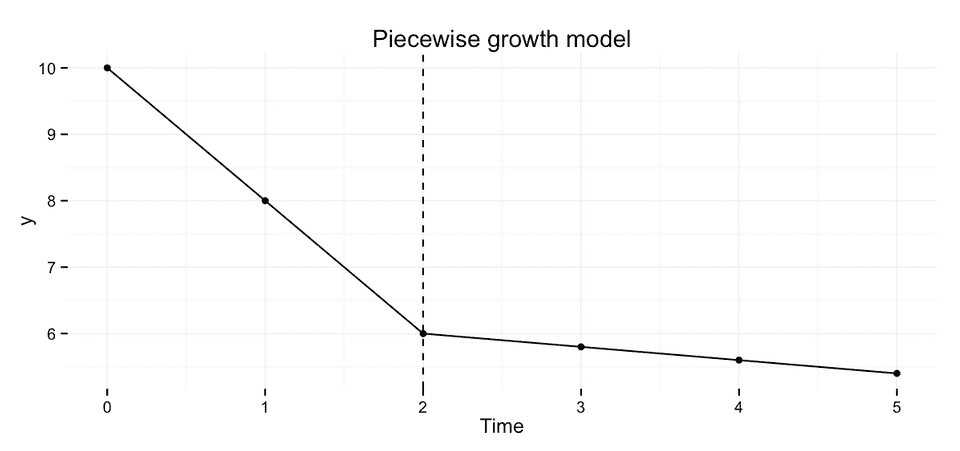
We could specify this model like this

Level 1 Y_{i j} Level 2 β_{0 j} β_{1 j} β_{2 j} = β_{0 j} + β_{1 j} t_{1 i j} + β_{2 j} t_{2 i j} + R_{i j} = γ_{00} + γ_{01} T X_{j} + U_{0 j} = γ_{10} + γ_{11} T X_{j} + U_{1 j} = γ_{20} + γ_{21} T X_{j} + U_{2 j}

with,

⎝ ⎛ U_{0 j} U_{1 j} U_{2 j} ⎠ ⎞ \sim N ⎝ ⎛ 000, τ_{00}^{2} τ_{01} τ_{02} τ_{01} τ_{10}^{2} τ_{12} τ_{02} τ_{12} τ_{20}^{2} ⎠ ⎞,

and

R_{i j} \sim N (0, σ^{2})

In this model I’ve fit the full level 2 variance-covariance matrix. If we wanted to fit this model we’d do it like this

Drop the correlation between time piece 1 and 2

Sometimes you might want to fit a model with a correlation between the random intercept and time piece 1, but no correlation between time piece 2 and the other effects. This would change the level 2 variance-covariance from above to this

⎝ ⎛ U_{0 j} U_{1 j} U_{2 j} ⎠ ⎞ \sim N ⎝ ⎛ 000, τ_{00}^{2} τ_{01} 0 τ_{01} τ_{10}^{2} 0 00 τ_{20}^{2} ⎠ ⎞

Fitting this model is straight-forward in lmer and more complicated in lme.

Adding a quadratic effect

We could extend the two-part piecewise growth model to allow for non-linear change during one or both of the pieces. As an example, I’ll cover extending the model to allow for quadratic change during piece 1.

Piecewise growth model with quadratic trend in R. By Kristoffer Magnusson

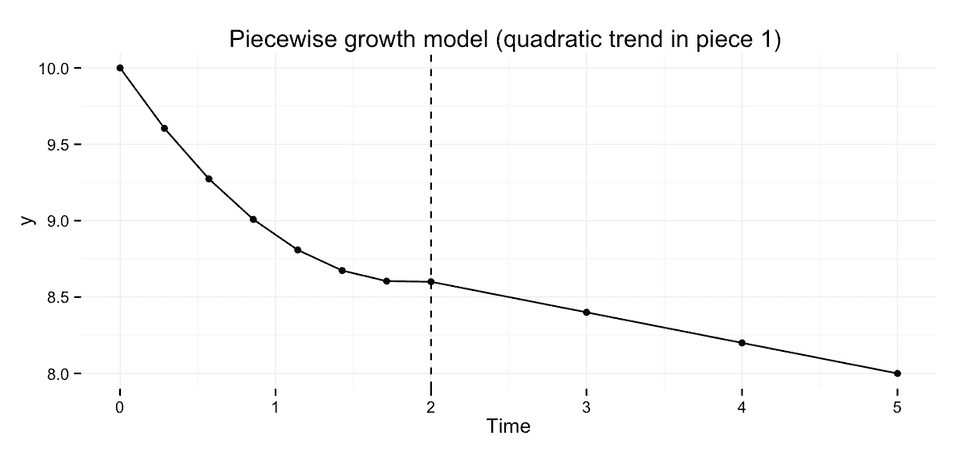
We could write this model like this

Level 1 Y_{i j} Level 2 β_{0 j} β_{1 j} β_{2 j} β_{3 j} = β_{0 j} + β_{1 j} t_{1} + β_{2 j} t_{1 i j}^{2} + β_{3 j} t_{2 i j} + R_{i j} = γ_{00} + γ_{01} T X_{j} + U_{0 j} = γ_{10} + γ_{11} T X_{j} + U_{1 j} = γ_{20} + γ_{21} T X_{j} + U_{2 j} = γ_{30} + γ_{31} T X_{j} + U_{3 j}

with,

⎝ ⎜ ⎜ ⎜ ⎛ U_{0 j} U_{1 j} U_{2 j} U_{3 j} ⎠ ⎟ ⎟ ⎟ ⎞ \sim N ⎝ ⎜ ⎜ ⎜ ⎛ 0000, τ_{00}^{2} τ_{01} τ_{02} τ_{03} τ_{01} τ_{10}^{2} τ_{12} τ_{13} τ_{02} τ_{12} τ_{20}^{2} τ_{23} τ_{03} τ_{13} τ_{23} τ_{30}^{2} ⎠ ⎟ ⎟ ⎟ ⎞,

and

R_{i j} \sim N (0, σ^{2})

This model could be fit like this

If you wanted to fit a reduced random effects structure you could use the method outlined in “Drop the correlation between time piece 1 and 2”.

Hypothesis tests

lmer does not report p-values or degrees of freedoms, see ?pvalues and r-sig-mixed-models FAQ for why not. However, there are other packages that will calculate p-values for you. I will cover some of them here.

Wald test

Likelihood ratio test

Profile confidence intervals

Parametric bootstrap

Kenward-Roger degrees of freedom approximation

Shattertwaite degrees of freedom approximation

Book recommendations

Not all of these books are specific to R and longitudinal data analysis. However, I’ve found them all useful over the years when working with multilevel/linear mixed models.

Singer & Wilett (2003). Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence
Pinheiro & Bates (2009). Mixed-Effects Models in S and S-PLUS (Statistics and Computing)
Hedeker & Gibsson (2006). Longitudinal Data Analysis
Fitzmaurice, Laird, & Ware (2011). Applied Longitudinal Analysis
Diggle et al (2013). Analysis of Longitudinal Data (Oxford Statistical Science Series)
Gelman & Hill (2006). Data Analysis Using Regression and Multilevel/Hierarchical Models
Raudenbush & Bryk (2001). Hierarchical Linear Models: Applications and Data Analysis Methods
Snijders & Bosker (2011). Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling
Hox, J (2010). Multilevel Analysis: Techniques and Applications, Second Edition
Goldstein, H (2010). Multilevel Statistical Models
Mirman (2014). Growth Curve Analysis and Visualization Using R
Finch, Bolin, & Kelley (2014). Multilevel Modeling Using R

Suggestions, errors or typos

Please don’t hesitate to contact me if you find some errors in this guide.

Written by Kristoffer Magnusson, a researcher in clinical psychology. You should follow him on Twitter and come hang out on the open science discord Git Gud Science.

Statistics Longitudinal Multilevel Linear mixed-effects model lme4 nlme Tutorial

Published April 21, 2015 (View on GitHub)

Buy Me A Coffee

Buy Me a Coffee ☕

(or use PayPal)

A huge thanks to the 152 supporters who've bought me a 361 coffees!

Jason Rinaldo bought ☕☕☕☕☕☕☕☕☕☕ (10) coffees

I've been looking for applets that show this for YEARS, for demonstrations for classes. Thank you so much! Students do not need to tolarate my whiteboard scrawl now. I'm sure they'd appreciate you, too.l

JDMM bought ☕☕☕☕☕ (5) coffees

You finally helped me understand correlation! Many, many thanks... 😄

@VicCazares bought ☕☕☕☕☕ (5) coffees

Good stuff! It's been so helpful for teaching a Psych Stats class. Cheers!

Dustin M. Burt bought ☕☕☕☕☕ (5) coffees

Excellent and informative visualizations!

Someone bought ☕☕☕☕☕ (5) coffees

@metzpsych bought ☕☕☕☕☕ (5) coffees

Always the clearest, loveliest simulations for complex concepts. Amazing resource for teaching intro stats!

Ryo bought ☕☕☕☕☕ (5) coffees

For a couple years now I've been wanting to create visualizations like these as a way to commit these foundational concepts to memory. But after finding your website I'm both relieved that I don't have to do that now and pissed off that I couldn't create anything half as beautiful and informative as you have done here. Wonderful job.

Diarmuid Harvey bought ☕☕☕☕☕ (5) coffees

You have an extremely useful site with very accessible content that I have been using to introduce colleagues and students to some of the core concepts of statistics. Keep up the good work, and thanks!

Michael Hansen bought ☕☕☕☕☕ (5) coffees

Keep up the good work!

Michael Villanueva bought ☕☕☕☕☕ (5) coffees

I wish I could learn more from you about stats and math -- you use language in places that I do not understand. Cohen's D visualizations opened my understanding. Thank you

Someone bought ☕☕☕☕☕ (5) coffees

Thank you, Kristoffer

Pål from Norway bought ☕☕☕☕☕ (5) coffees

Great webpage, I use it to illustrate several issues when I have a lecture in research methods. Thanks, it is really helpful for the students:)

@MAgrochao bought ☕☕☕☕☕ (5) coffees

Joseph Bulbulia bought ☕☕☕☕☕ (5) coffees

Hard to overstate the importance of this work Kristoffer. Grateful for all you are doing.

@TDmyersMT bought ☕☕☕☕☕ (5) coffees

Some really useful simulations, great teaching resources.

@lakens bought ☕☕☕☕☕ (5) coffees

Thanks for fixing the bug yesterday!

@LinneaGandhi bought ☕☕☕☕☕ (5) coffees

This is awesome! Thank you for creating these. Definitely using for my students, and me! :-)

@ICH8412 bought ☕☕☕☕☕ (5) coffees

very useful for my students I guess

@KelvinEJones bought ☕☕☕☕☕ (5) coffees

Preparing my Master's student for final oral exam and stumbled on your site. We are discussing in lab meeting today. Coffee for everyone.

Someone bought ☕☕☕☕☕ (5) coffees

What a great site

@Daniel_Brad4d bought ☕☕☕☕☕ (5) coffees

Wonderful work!

David Loschelder bought ☕☕☕☕☕ (5) coffees

Terrific work. So very helpful. Thank you very much.

@neilmeigh bought ☕☕☕☕☕ (5) coffees

I am so grateful for your page and can't thank you enough!

@giladfeldman bought ☕☕☕☕☕ (5) coffees

Wonderful work, I use it every semester and it really helps the students (and me) understand things better. Keep going strong.

Dean Norris bought ☕☕☕☕☕ (5) coffees

Sal bought ☕☕☕☕☕ (5) coffees

Really super useful, especially for teaching. Thanks for this!

dde@paxis.org bought ☕☕☕☕☕ (5) coffees

Very helpful to helping teach teachers about the effects of the Good Behavior Game

@akreutzer82 bought ☕☕☕☕☕ (5) coffees

Amazing visualizations! Thank you!

@rdh_CLE bought ☕☕☕☕☕ (5) coffees

So good!

Amanda Sharples bought ☕☕☕ (3) coffees

Soyol bought ☕☕☕ (3) coffees

Someone bought ☕☕☕ (3) coffees

Kenneth Nilsson bought ☕☕☕ (3) coffees

Keep up the splendid work!

@jeremywilmer bought ☕☕☕ (3) coffees

Love this website; use it all the time in my teaching and research.

Someone bought ☕☕☕ (3) coffees

Powerlmm was really helpful, and I appreciate your time in putting such an amazing resource together!

DR AMANDA C DE C WILLIAMS bought ☕☕☕ (3) coffees

This is very helpful, for my work and for teaching and supervising

Georgios Halkias bought ☕☕☕ (3) coffees

Regina bought ☕☕☕ (3) coffees

Love your visualizations!

Susan Evans bought ☕☕☕ (3) coffees

Thanks. I really love the simplicity of your sliders. Thanks!!

@MichaMarie8 bought ☕☕☕ (3) coffees

Thanks for making this Interpreting Correlations: Interactive Visualizations site - it's definitely a great help for this psych student! 😃

Zakaria Giunashvili, from Georgia bought ☕☕☕ (3) coffees

brilliant simulations that can be effectively used in training

Someone bought ☕☕☕ (3) coffees

@PhysioSven bought ☕☕☕ (3) coffees

Amazing illustrations, there is not enough coffee in the world for enthusiasts like you! Thanks!

Cheryl@CurtinUniAus bought ☕☕☕ (3) coffees

🌟What a great contribution - thanks Kristoffer!

vanessa moran bought ☕☕☕ (3) coffees

Wow - your website is fantastic, thank you for making it.

Someone bought ☕☕☕ (3) coffees

mikhail.saltychev@gmail.com bought ☕☕☕ (3) coffees

Thank you Kristoffer This is a nice site, which I have been used for a while. Best Prof. Mikhail Saltychev (Turku University, Finland)

Someone bought ☕☕☕ (3) coffees

Ruslan Klymentiev bought ☕☕☕ (3) coffees

@lkizbok bought ☕☕☕ (3) coffees

Keep up the nice work, thank you!

@TELLlab bought ☕☕☕ (3) coffees

Thanks - this will help me to teach tomorrow!

SCCT/Psychology bought ☕☕☕ (3) coffees

Keep the visualizations coming!

@elena_bolt bought ☕☕☕ (3) coffees

Thank you so much for your work, Kristoffer. I use your visualizations to explain concepts to my tutoring students and they are a huge help.

A random user bought ☕☕☕ (3) coffees

Thank you for making such useful and pretty tools. It not only helped me understand more about power, effect size, etc, but also made my quanti-method class more engaging and interesting. Thank you and wish you a great 2021!

@hertzpodcast bought ☕☕☕ (3) coffees

We've mentioned your work a few times on our podcast and we recently sent a poster to a listener as prize so we wanted to buy you a few coffees. Thanks for the great work that you do!Dan Quintana and James Heathers - Co-hosts of Everything Hertz

Cameron Proctor bought ☕☕☕ (3) coffees

Used your vizualization in class today. Thanks!

eshulman@brocku.ca bought ☕☕☕ (3) coffees

My students love these visualizations and so do I! Thanks for helping me make stats more intuitive.

Someone bought ☕☕☕ (3) coffees

Adrian Helgå Vestøl bought ☕☕☕ (3) coffees

@misteryosupjoo bought ☕☕☕ (3) coffees

For a high school teacher of psychology, I would be lost without your visualizations. The ability to interact and manipulate allows students to get it in a very sticky manner. Thank you!!!

Chi bought ☕☕☕ (3) coffees

You Cohen's d post really helped me explaining the interpretation to people who don't know stats! Thank you!

Someone bought ☕☕☕ (3) coffees

You doing useful work !! thanks !!

@ArtisanalANN bought ☕☕☕ (3) coffees

Enjoy.

@jsholtes bought ☕☕☕ (3) coffees

Teaching stats to civil engineer undergrads (first time teaching for me, first time for most of them too) and grasping for some good explanations of hypothesis testing, power, and CI's. Love these interactive graphics!

@notawful bought ☕☕☕ (3) coffees

Thank you for using your stats and programming gifts in such a useful, generous manner. -Jess

Mateu Servera bought ☕☕☕ (3) coffees

A job that must have cost far more coffees than we can afford you ;-). Thank you.

@cdrawn bought ☕☕☕ (3) coffees

Thank you! Such a great resource for teaching these concepts, especially CI, Power, correlation.

Julia bought ☕☕☕ (3) coffees

Fantastic work with the visualizations!

@felixthoemmes bought ☕☕☕ (3) coffees

@dalejbarr bought ☕☕☕ (3) coffees

Your work is amazing! I use your visualizations often in my teaching. Thank you.

@PsychoMouse bought ☕☕☕ (3) coffees

Excellent! Well done! SOOOO Useful!😊 🐭

Dan Sanes bought ☕☕ (2) coffees

this is a superb, intuitive teaching tool!

@whlevine bought ☕☕ (2) coffees

Thank you so much for these amazing visualizations. They're a great teaching tool and the allow me to show students things that it would take me weeks or months to program myself.

Someone bought ☕☕ (2) coffees

@notawful bought ☕☕ (2) coffees

Thank you for sharing your visualization skills with the rest of us! I use them frequently when teaching intro stats.

Andrew J O'Neill bought ☕ (1) coffee

Thanks for helping understand stuff!

Someone bought ☕ (1) coffee

Shawn Hemelstrand bought ☕ (1) coffee

Thank you for this great visual. I use it all the time to demonstrate Cohen's d and why mean differences affect it's approximation.

Adele Fowler-Davis bought ☕ (1) coffee

Thank you so much for your excellent post on longitudinal models. Keep up the good work!

Stewart bought ☕ (1) coffee

This tool is awesome!

Someone bought ☕ (1) coffee

Aidan Nelson bought ☕ (1) coffee

Such an awesome page, Thank you

Someone bought ☕ (1) coffee

Ellen Kearns bought ☕ (1) coffee

Dr Nazam Hussain bought ☕ (1) coffee

Someone bought ☕ (1) coffee

Eva bought ☕ (1) coffee

I've been learning about power analysis and effect sizes (trying to decide on effect sizes for my planned study to calculate sample size) and your Cohen's d interactive tool is incredibly useful for understanding the implications of different effect sizes!

Someone bought ☕ (1) coffee

Thanks a lot!

Someone bought ☕ (1) coffee

Reena Murmu Nielsen bought ☕ (1) coffee

Tony Andrea bought ☕ (1) coffee

Thanks mate

Tzao bought ☕ (1) coffee

Thank you, this really helps as I am a stats idiot :)

Melanie Pflaum bought ☕ (1) coffee

Sacha Elms bought ☕ (1) coffee

Yihan Xu bought ☕ (1) coffee

Really appreciate your good work!

@stevenleung bought ☕ (1) coffee

Your visualizations really help me understand the math.

Junhan Chen bought ☕ (1) coffee

Someone bought ☕ (1) coffee

Michael Hansen bought ☕ (1) coffee

ALEXANDER VIETHEER bought ☕ (1) coffee

mather bought ☕ (1) coffee

Someone bought ☕ (1) coffee

Bastian Jaeger bought ☕ (1) coffee

Thanks for making the poster designs OA, I just hung two in my office and they look great!

@ValerioVillani bought ☕ (1) coffee

Thanks for your work.

Someone bought ☕ (1) coffee

Great work!

@YashvinSeetahul bought ☕ (1) coffee

Someone bought ☕ (1) coffee

Angela bought ☕ (1) coffee

Thank you for building such excellent ways to convey difficult topics to students!

@inthelabagain bought ☕ (1) coffee

Really wonderful visuals, and such a fantastic and effective teaching tool. So many thanks!

Someone bought ☕ (1) coffee

Yashashree Panda bought ☕ (1) coffee

I really like your work.

Ben bought ☕ (1) coffee

You're awesome. I have students in my intro stats class say, "I get it now," after using your tool. Thanks for making my job easier.

Gabriel Recchia bought ☕ (1) coffee

Incredibly useful tool!

Shiseida Sade Kelly Aponte bought ☕ (1) coffee

Thanks for the assistance for RSCH 8210.

@Benedikt_Hell bought ☕ (1) coffee

Great tools! Thank you very much!

Amalia Alvarez bought ☕ (1) coffee

@noelnguyen16 bought ☕ (1) coffee

Hi Kristoffer, many thanks for making all this great stuff available to the community!

Eran Barzilai bought ☕ (1) coffee

These visualizations are awesome! thank you for creating it

Someone bought ☕ (1) coffee

Chris SG bought ☕ (1) coffee

Very nice.

Gray Church bought ☕ (1) coffee

Thank you for the visualizations. They are fun and informative.

Qamar bought ☕ (1) coffee

Tanya McGhee bought ☕ (1) coffee

@schultemi bought ☕ (1) coffee

Neilo bought ☕ (1) coffee

Really helpful visualisations, thanks!

Someone bought ☕ (1) coffee

This is amazing stuff. Very slick.

Someone bought ☕ (1) coffee

Sarko bought ☕ (1) coffee

Thanks so much for creating this! Really helpful for being able to explain effect size to a clinician I'm doing an analysis for.

@DominikaSlus bought ☕ (1) coffee

Thank you! This page is super useful. I'll spread the word.

Someone bought ☕ (1) coffee

Melinda Rice bought ☕ (1) coffee

Thank you so much for creating these tools! As we face the challenge of teaching statistical concepts online, this is an invaluable resource.

@tmoldwin bought ☕ (1) coffee

Fantastic resource. I think you would be well served to have one page indexing all your visualizations, that would make it more accessible for sharing as a common resource.

Someone bought ☕ (1) coffee

Fantastic Visualizations! Amazing way to to demonstrate how n/power/beta/alpha/effect size are all interrelated - especially for visual learners! Thank you for creating this?

@jackferd bought ☕ (1) coffee

Incredible visualizations and the best power analysis software on R.

Cameron Proctor bought ☕ (1) coffee

Great website!

Someone bought ☕ (1) coffee

Hanah Chapman bought ☕ (1) coffee

Thank you for this work!!

Someone bought ☕ (1) coffee

Jayme bought ☕ (1) coffee

Nice explanation and visual guide of Cohen's d

Bart Comly Boyce bought ☕ (1) coffee

thank you

Dr. Mitchell Earleywine bought ☕ (1) coffee

This site is superb!

Florent bought ☕ (1) coffee

Zampeta bought ☕ (1) coffee

thank you for sharing your work.

Mila bought ☕ (1) coffee

Thank you for the website, made me smile AND smarter :O enjoy your coffee! :)

Deb bought ☕ (1) coffee

Struggling with statistics and your interactive diagram made me smile to see that someone cares enough about us strugglers to make a visual to help us out!😍

Someone bought ☕ (1) coffee

@exerpsysing bought ☕ (1) coffee

Much thanks! Visualizations are key to my learning style!

Someone bought ☕ (1) coffee

Webmentions

0 0

What's this?

マルオウン 2023-03-19

Using R and lme/lmer to fit different two- and three-level longitudinal models rpsychologist.com/r-guide-longit…

Solomon Kurz 2022-11-29

Not this time. The model takes a while to run. However, the data are open and I will eventually post them and the analysis code on GitHub--maybe within the next week or so. You can read about level-2 and 3 SDs in any good book on multilevel models. Also: rpsychologist.com/r-guide-longit…

Ekaterina Pronizius 2021-05-04

Using R and lme/lmer to fit different two- and three-level longitudinal models rpsychologist.com/r-guide-longit…

(Webmentions sent before 2021 will unfortunately not show up here.)

Archived Comments (41)

Vincent Isoz 2019-07-17

What book or PDF would you recommend to have very extremely mathematical details on longitudinal analysis (all steps of proofs given). Whatever the level, basics or advanced? Thx

Keith Goldfeld 2019-06-18

Kristoffer -

This is a really useful post, which I know you did quite a while ago. I was wondering if you have come across a situation where you needed to impose structure on the correlation of the random effects (of the 2nd level of a 2-level model). In my case, I have measurement periods (and individuals are measured only once. There is a cluster-specific effect in each period (U_t, t in (0,1,2,3,4)), and these cluster specific effects are correlated; in particular, the correlations degrade over time (AR1). I don't believe lme4 or nlme can accomdoate this, but thought maybe you would correct me if I am wrong.

- Keith

Shalini Kurumathur 2019-04-13

Thank you for such a great website. I understood the three level equations because of this website. I am working on a educational data: three-level discontinuous growth model. I have an issue in the code using control variables. ses(Socio economic status),lcsize(class size) are time variant control variables and demo(demographic such as urban/rural-as 0,1) is time-invariant control variable. After the null model, I used this code. Not sure if this is right. PERF85 is the dependent variable, TIME,TRANS and RECOV are independent variable. I am not getting any error though-
step1a <-lme(PERF85~TIME+TRANS+RECOV+ses+lcsize, random=~1|ENTITY_CD,FINNL85,
control=lmeControl(opt="optim"))
while using (TIME|ses) or (1|ses) I am getting error

Sketching Sketcher 2019-03-05

This is very useful! THanks!

Marcos Salvino 2019-02-20

Dear Kristoffer,

Thank you for this website. I tried to follow your commands (in R), but I didn't get your data. Please, can you show how to get your data? I'm trying to understand your thoughts. Thank you in advance, Marcos Salvino

radek 2019-01-31

Hi Kristoffer. How would go about fitting quadratic trend for data without tx? Should that simply be removed from equation?

lmer(y ~ (time + I(time^2)) + (time + I(time^2) | subjects), data=data)

Also, how can one access the results for plotting temporal effect on graphs as you do it?

Many thanks!

Mirjam Moerbeek 2018-10-31

Dear Kristoffer,
Thank you for this great website. I have a question on the partially nested models. What value should you use for the grouping variable "therapist" for those subjects who are in the control condition (i.e. for those subjects who are not nested within therapists). I have seen various suggestions: the control subjects are all in clusters of size 1, the control subjects are all in one large cluster, use the value "none" for the control subjects. What would you recommend?
Thanks in advance,
Mirjam Moerbeek

Kristoffer Magnusson 2018-10-31

Hi Mirjam, that's a great question and something I've been planning on clarifying in this post. As long as the indicator variable (control = 0) is included in the random effects formula all the third-level random effects will be zero in the control group, for all the coding suggestions you mention. Using this parameterization, it is my experience that the choice of coding will make no practical difference on the estimates (at least when using lme4). Using the value "none" (character) will be equivalent to coding it as one large cluster. For practical reasons, I tend to code them as being in 1 large cluster, or sometimes (if it is a simulation) as belonging to the same number of clusters as the treatment group. The model will fit slightly faster compared to using singletons, and ranef() and coef() will only include 1 row third level for the control group.

For clarification, here's a small example using powerlmm


library(powerlmm)
library(lmerTest)
library(dplyr)

## Partially nested DGP
## random intercept and slope at both lvl 2 and 3
p <- study_parameters(n1 = 11,
                      n2 = 50, 
                      n3 = 4, 
                      partially_nested = TRUE, 
                      icc_pre_subject = 0.5, 
                      icc_pre_cluster = 0.1, 
                      icc_slope = 0.02,
                      var_ratio = 0.02)
set.seed(4545)
d <- simulate_data(p)

# 4 "pseudo-clusters" in control group
d %>% 
    group_by(treatment, cluster) %>% 
    summarise(n = n()/11)
fit <- lmer(y ~ time * treatment + (time | subject) + (0 + treatment + treatment:time | cluster), data = d)

# Recode to 1 cluster in control group
d2 <- d
d2 %>% 
    group_by(treatment, cluster) %>% 
    summarise(n = n()/11)
d2[d2$treatment == 0, "cluster"] <- 1

fit2 <- lmer(y ~ time * treatment + (time | subject) + (0 + treatment + treatment:time | cluster), data = d2)

# Recode to singletons
d3 <- d
d3 %>% 
    group_by(treatment, cluster) %>% 
    summarise(n = n()/11)
d3[d3$treatment == 0, "cluster"] <- d3[d3$treatment == 0, "subject"] 

fit3 <- lmer(y ~ time * treatment + (time | subject) + (0 + treatment + treatment:time | cluster), data = d3)

# Fixef variances
identical(vcov(fit), vcov(fit2)) # TRUE
identical(vcov(fit), vcov(fit3)) # FALSE

# Extremely small diff for time:treatment variance
(vcov(fit)[4,4] - vcov(fit3)[4,4])/(vcov(fit)[4,4])

ranef(fit)$cluster
ranef(fit2)$cluster
ranef(fit3)$cluster

# Identical deviances
REMLcrit(fit)
REMLcrit(fit2)
REMLcrit(fit3)

Mirjam Moerbeek 2018-11-02

Dear Kristoffer,
Thanks for the prompt reply! I have simulated some large data sets for different specifications of the therapist variable and the results are conform your answer.
Best wishes,
Mirjam

Johanna TJ 2018-10-30

Hi Kristoffer,
I have another question regarding centering. I was wondering whether I need to additionally center time (e.g. grand mean centering) if I use {0,1,2,2,2} and {0,0,0,1,2} as the two time periods? Or does this automatically mean that time was centered at the third time point so that this time point served as zero?
J.

Gabbie 2018-08-07

Hi Kristoffer
This article was very timely as I am in the process of analyzing the data for my first PhD study. Could you explain further what you mean by " In scheme 1 the two slope coefficients represent the actual slope in the respective time period. Whereas in scheme 2 the coefficient for time 2 represents the deviation from the slope in period 1, i.e. if the estimate is 0 then the rate of change is the same in both periods."

I understand in scheme 1, you compare slopes created by time points 0:2 to 3:5. Scheme 2 is a little confusing. Are you saying that here you comparing a hypothetical slope 3:5 (based on what would be expected given slope 0:2) to 3:5?

I was also wondering whether you could describe how to code three growth curves (i.e. my data has two discontinuities) using both schemes you described above. I have data with 15 time points (0:14). At time points 5:7 there was an experimental manipulation which created a downward shift from time point 4 to 5, and then an upward shift from point 7 to 8.

Most of the studies I've looked at for examples only have a single discontinuity or do not adequately describe how they coded their variables.

Cheers

Johanna TJ 2018-07-17

Hi Kristoffer, I am currently working on a 2-level piecewise growth model with two separate slopes and I was using your coding scheme 1 which was really helpful! Could you provide a reference in which this coding scheme was introduced?
Thanks,
J.

Kristoffer Magnusson 2018-07-17

Hi Johanna, the coding scheme is from Raudenbush & Bryk (2001) p 179.

Johanna TJ 2018-07-18

Great, thanks a lot!

Slobodan Ivanovic 2018-06-23

Hi Kristoffer, excellent post. Do you know how to implement multiple membership with lme4? Grettings

Kristoffer Magnusson 2018-06-24

Thanks! Last time I checked fitting a multiple membership model in lme4 required some hacking, however that was several years ago. brms or MCMCglmm are probably better options, see brms::mm or MCMCglmm::mult.memb

Slobodan Ivanovic 2018-06-24

Thank you!

saddas 2018-05-14

Hi Kristoffer,
I am wondering if R can handle a 3-level multilevel model where the DV is a count variable (i.e., a GLMM model). I know that this is not possible in SAS in Proc GLIMMIX.
Thanks.
Shamel

Kristoffer Magnusson 2018-05-15

Hi, you can use lme4 to fit 3-level GLMMs just replace "lmer" with "glmer", and add the "family" argument.

saddas 2018-05-15

Thanks, Kristoffer. As far as I know, glmer (lme4 package) does not allow us to specify a structure for the residual (R) matrix. If this is correct, is there any way to model 3 levels of nesting using NLME, which has flexibility in specifying the R matrix?

Kristoffer Magnusson 2018-05-15

That is correct, lme4 does not support R-side effects. You could try MASS::glmmPQL which allows fitting GLMMs with R-side effects using nlme under the hood.

saddas 2018-05-15

Thanks, 2 quick follow up questions:
(1) When you say lme4 dos not support R-side effects, does this mean it can only model a residual matrix with constant variances and zero covariances (i.e., a variance components matrix)?

(2) Does glmmPQL allow for fitting models with 3 levels of nesting? ?I couldn't find anything in the documentation on this.

Vijay 2017-11-22

Hi Kristoffer,
First of all thank you for this guide.
This is very useful guide.
I have one question regarding Two-level model.
Actually i have data with two group of treatment having repeated measurements. Total sample size is 50, 25 each group and repeated measurements taken 14 times each individual. I want to apply two level model on this data. I want to check which treatment is better. i want to keep repeated measurements of an individual at level one. Could you plese help me out for this issue.
Thanks in advance.

Best,
Vijay

JayZ 2017-10-20

HI Kristoffer,

I was wondering about the piecewise fitting of time variable... I have a dataset where the time points are 1:60 days and every 2 or 3 days(so not 1,2,3 etc but 1,3,5,8 etc), and unequal between subjects. I tried to use the second format as you present it here, and then fit the model, but i get a rank-defficient error in lmer, and a singularity error in lme... Do you have an idea of solving that ?

Thanks a lot,
John

Pablo Beltramone 2017-09-07

Hi Kristoffer

Thanks a lot for this guide. I really really need your help with an issue: I need to fit a model whit time series data, like a mixed model. I have the hourly arrivals of costumes that enter to a company. I'm trying to fit a mixed model with FE such the day of the week and the hour of the day. As ME I'm trying to to estimate an ar(1) covar matrix for within day (5 hours from open to close time, so 5x5 matrix) and a ar(1) covar matrix for between days (5 days a week, so 5x5 matrix), so my data is:

date day houre CantCustomers
1/1/2014 1 10 125
1/1/2014 1 11 110
1/1/2014 1 12 180
1/1/2014 1 13 173
1/1/2014 1 14 68
2/1/2014 2 10 114
2/1/2014 2 11 92
...

My model in R is actualy:
y <= lme(CantCustomer ~ daynum + houre, random=~1|date,correlation = corAR(1),data = datosh)

When I check the R matrix it is of 5x5. But the D matrix gave me just 1 value, de variance. I understand that this is a sigma*Identity of 5x5. The matrix is then the result of V = Z'DZ + R and also a 5x5 matrix.
How can I set the R and D matrix in order to fit the hourly (intra) and daily (between) covariance matrix like a Ar(1)?

Thank you very much, any tip can help.

James 2017-06-29

This is such a good blog content that shows some great learning to us. Good thing that you have able to give some values terms about using the hierarchical linear models in solving problems like this. This gives an ideal learning to us.

Chao Liu 2017-05-17

Hi Kristoffer,

Thank you for sharing this! It definitely became one of my must-turn-to references for doing longitudinal models in R. I just have a quick maybe unrelated question: so how to do a multilevel time series analysis (N>1) in R? What packages can be used for that?

Thanks in advance!

Chao

Sergio Francisco Juárez Cerril 2017-05-16

Very helpful. Thanks!

Rebecca Steingut 2016-07-28

Hi Kirstoffer,

Thanks so much for the impressively educational page.

I am not sure you will be able to answer this, but I thought I might try.

I am specifying a model with data that includes observations within subjects within therapists. We include a random intercept for subjects and one for therapists. The syntax for the random effects looks like this:

/RANDOM=INTERCEPT | SUBJECT(ther) COVTYPE(VC)
/RANDOM=INTERCEPT | SUBJECT(ther*subject) COVTYPE(VC)
/REPEATED=time | SUBJECT(ther*subject) COVTYPE(AR1).

I'm pretty sure I figured out that the intercepts would look like this
(1 |ther:subject) +(1|ther),).

However, our model is not a growth model. We aren't interested in change over time. Rather, we include time as a covariate in the model to estimate the effects controlling for the time variable. I know how to include time as a covariate, but I'm not sure where to specify the information about time being a repeated measure.

Any help you can offer is appreciated!

Sarah Landmann 2016-04-01

Hi Kristoffer,
I am so glad that I found your guide; it is extremely helpful to have a tutorial for fitting multilevel models for a two-group repeated measurements design! Thanks a lot!
I have only two questions and would be grateful if you could help me with that:
If I get it right, the conditional growth model includes an interaction term group*time and a random part allowing subjects to have individual intercepts and individual slopes for the effect of time on this dependent variable, right?
In some tutorials I have seen that they add a "1+" (1+time|subjects) instead of only (time|subjects). What is the difference here?
My second question is: Against which model would I have to test this model In a likelihood ratio test in order to test that the interaction "group*time" is significant (which is actually what I am interested in, compared to the effect of either group or time)? Should I compare it against a model that only includes an additive term for group and time as predictors? Or against the "intercept-only model" lmer(y ~ 1 + (1 | subjects)?
Thanks a lot!
Sarah

BERNA ARSLAN UZUNDAG 2016-03-15

Hi Kristoffer, I found this page very useful. I'm trying to fit a piecewise growth curve model to my data using lme. I coded the time variable as you suggested (option 2). But still I'm not sure how to interpret the findings. If the slope of time2 is very close to 0 but not equal to 0, does it still mean that the slope in time2 is not different from the slope in time1? Is there a test to compare the slopes? Thank you.

Eiko Fried 2016-03-03

Thanks for the great guide. I have a few follow up questions:
(1) What package can model the above in case of ordinal data (with 3-4 categories)?
(2) How do these methods deal with missing data?
(3) Can one model 2 or 3 dependent variables at the same time?

Thanks!
Eiko

Massil Benbouriche 2016-02-10

Hi Kristoffer,

A very simple question .In your first example, can we imagine to treat the treatment groups (Treatment vs. control) as a third-level = Repeated measures nested in subjects nested in one of the 2 groups ?

Or do we have to treat the treatment groups as a 2nd-level predictor due to random assigment ? After all, except the assignment to one of the two groups (that we can easily control), we don't have any other kind of clustering that would justify to treat the Treatment groups as a 3rd-level.

Many thanks for your post.

Massil

Xiaoxin 2016-01-12

Thank you, Kristoffer, for posting this guide. That's really helpful. There is one thing that confuses me about the "conditional growth model". At level 2 of the model, the model formulation sets the data level for TX at subject[j], so that we should interpret the coefficient of gamma[01] as the effect of TX on subject j's average Y. Is my understanding right?
But when put this model formulation into the "lmer", we have data level for TX at [i] but not at subject [j]. That's we actually have for the full model formulation in "lmer" is: Y[ij] ~ gamma[00] + gamma[01]*TX[ij] +
U[0j] + gamma[10] + gamma[11]*TX [i,j] + U[1j]. Then, here, we have different interpretation of gamma[01], it is the effect of [i]'s TX on Y[i]. That means the original model formulation (equation 11) is inconsistent with what you did in "lmer". Is my understanding right?
I understand that each subject[j] has the same TX. But I think equation 11 is a kind of a regression doing "Average of Y at subject [j] ~ TX[j]"; the lmer is doing a different regression as "Observed Y at [i] of subject [j] ~ TX[ij]". They are two different things.

I am sorry for distracting you with this question. But this question came out of me when reading your guide, and I really want to figure out it.

I look forward to your reply.

Best regards,
Xiaoxin

Paquito Bernard 2016-01-05

Second time that your website is VERY useful to check my syntax ! I am
working on three arms RCT (tx1 vs. tx2 vs. control). Evertything is OK
but I can't "see" the control in my output (i.e., summary(lme) Do you
have any idea ? Thank you again

Allan Debertin 2015-12-13

Great post.

Question. Can you use this design with continuous data? What if treatment was of different dosages, 0.1, 0.2, 0.3 mg? I guess you could use a discrete value to categorize the treatments...

A better question then is, what if treatment was different dosages, and those dosages varied through measuring a subjects response? Say 0.1mg for the first observation, 0.3mg for the second observation and 0.1mg for the third observation?

I'm looking to use a longitudinal design to understand growth patterns in a salmon population. We have repeated measures of growth of the salmon. We expect that a slower rate of growth of salmon when there are more salmon (competition for food) and a faster rate of growth when there are fewer salmon. My treatment variable would be a continuous distribution of salmon abundance for different observations, I could make this a discrete variable I suppose, but then I still run into the same problem that treatment is varying throughout the observations of an individual. Do you think the longitudinal approach still applies?

MSFM 2015-09-02

Hi Kristoffer, thanks for the post!
I have a general question. Suppose we have data of individuals nested by households and also this data was gathered in different days across one year. We believe that there are season as well as day effects. Also, we acknowledge the natural nesting structure of the data (i.e. persons in households). Can I estimate a multilevel model where I specify:
lmer(y~1+(1|household/person)+(1|Day/Season), data=mydata)
Basically, I am trying to capture the correlation in ys of the persons in the same household as well the correlation across same days of the week across the same season. And the between household and season effect .. does that make sense? Am I specifying the model correctly?

Krishna Karthik 2015-05-21

Hi, First of all, thank you very much for posting this guide. I cannot express how much this has helped in me in my work! Second, towards the very end of the post, you gave out several suggestions for hypothesis testing, and mentioned that in the 'lme4' package, performing a 'summary' of the LMER model would give p-values of Wald tests. Or did you mean the test statistic only?

Also, can you point me to a source that explains in a simplified manner why the lmer model does not give p-values? Douglas Bates' book explains it, but it is more math heavy and I could barely follow it. Thanks again!!

Kristoffer Magnusson 2015-05-21

Glad you found this post helpful! To get p-values by using summary() on lme4-objects you need to install and load the lmerTest-package. Once its loaded you can use lmer() and summary() as you normally do.

Regarding why p-values are not reported there's an explanation in in the r-sig-mixed-models FAQ http://glmm.wikidot.com/faq...

Shayna Williams-Burris 2016-03-03

Thanks for this! It's very helpful to understand both functions and how to use their more advanced/complex capabilities. I'm a little confused, though, about the p-values. If I run lme from the nlme package it gives me p-values, and if I run lmer from the lme4 package for the same model and then use lmerTest to get p-values the values do not match with the lme p-values. Most are similar, but in some cases it's the difference between significance or not for very important measures. How do I reconcile this difference? Is one "more" correct?

I'm looking at:

#lme
library(nlme)
model1<-lme(value ~ Sex * Genotype * Gonad * time, random = ~ time | ID, data = my.data)
anova(model1)

vs.

#lmer
library(lme4)
library(lmerTest)
model2<-lmer(value ~ Sex * Genotype * Gonad * time + (time | ID), data = my.data)
anova(model2)

Krishna Karthik 2015-05-20

Thank you so much for this!! I cannot express how much easier you have made my life by posting these. However, I have one question. The summary command on the lmer model does not seem to have Wald tests in the output, any idea why? Or how I can get them?

subjects	tx	therapist	time	y
1	0	1	0	10
1	0	1	1	12
1	0	1	2	14
2	0	1	0	4
2	0	1	1	14
2	0	1	2	13
3	0	2	0	12
3	0	2	1	15
3	0	2	2	16
4	0	2	0	17
4	0	2	1	13
4	0	2	2	12
5	0	3	0	15
5	0	3	1	13
…	…	…	…	…

subjects	tx	therapist	time	y
1	0	1	0	10
1	0	1	1	12
1	0	1	2	14
2	0	1	0	4
2	0	1	1	14
2	0	1	2	13
3	0	2	0	12
3	0	2	1	15
3	0	2	2	16
4	0	2	0	17
4	0	2	1	13
4	0	2	2	12
5	0	3	0	15
5	0	3	1	13
…	…	…	…	…

Using R and lme/lmer to fit different two- and three-level longitudinal models

Data format

Power analysis, and simulating these models

Longitudinal two-level model

Unconditional model

Unconditional growth model

Conditional growth model

Conditional growth model: dropping random slope

Conditional growth model: dropping random intercept

Conditional growth model: dropping intercept-slope covariance

Three-level models

Conditional three-level growth model

Subject level randomization (therapist crossed effect)

Different level 3 variance-covariance matrix

Partially nested models

More on level 1 specification

Heteroscedasticity at Level 1

More grouping

First-order Autoregressive AR(1) residuals

Heterogenous AR(1)

More level 1 variance-covariances matrices

Changing the functional form of time

Quadratic trend

Orthogonal polynomials

Piecewise growth curve

Coding scheme 1: separate slopes

Coding scheme 2: incremental/decremental slope

Drop the correlation between time piece 1 and 2

Adding a quadratic effect

Hypothesis tests

Wald test

Likelihood ratio test

Profile confidence intervals

Parametric bootstrap

Kenward-Roger degrees of freedom approximation

Shattertwaite degrees of freedom approximation

Book recommendations

Suggestions, errors or typos

Buy Me A Coffee

Sponsors

Questions & Comments

Webmentions

Archived Comments (41)

subjects	tx	therapist	time	y
1	0	1	0	10
1	0	1	1	12
1	0	1	2	14
2	0	1	0	4
2	0	1	1	14
2	0	1	2	13
3	0	2	0	12
3	0	2	1	15
3	0	2	2	16
4	0	2	0	17
4	0	2	1	13
4	0	2	2	12
5	0	3	0	15
5	0	3	1	13
…	…	…	…	…