Understanding Maximum Likelihood

An Interactive Visualization

The maximum likelihood method is used to fit many models in statistics. In this post I will present some interactive visualizations to try to explain maximum likelihood estimation and some common hypotheses tests (the likelihood ratio test, Wald test, and Score test).

We will use a simple model with only two unknown parameters: the mean and variance. Our primary focus will be on the mean and we'll treat the variance as a nuisance parameter.

Likelihood Calculation

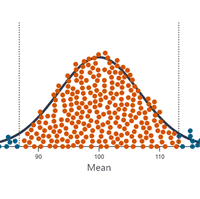
Before we do any calculations, we need some data. So, here's 10 random observations from a normal distribution with unknown mean (μ) and variance (σ²).

Y = [1.0, 2.0]

We also need to assume a model, we're gonna go with the model that we know generated this data: $y \sim \mathcal N(\mu, \sigma^2)$ . The challenge now is to find what combination of values for μ and σ² maximize the likelihood of observing this data (given our assumed model). Try moving the sliders around to see what happens.

Mean (μ)

Variance (σ²)

We can calculate the joint likelihood by multiplying the densities for all observations. However, often we calculate the log-likelihood instead, which is

$\ell(\mu, \sigma^2) = \sum_i^n \text{ln} \thinspace f_y(y_i)=$ -34.4+-33.6=-68.1

The combination of parameter values that give the largest log-likelihood is the maximum likelihood estimates (MLEs).

Finding the Maximum Likelihood Estimates

Since we use a very simple model, there's a couple of ways to find the MLEs. If we repeat the above calculation for a wide range of parameter values, we get the plots below. The joint MLEs can be found at the top of contour plot, which shows the likelihood function for a grid of parameter values. We can also find the MLEs analytically by using some calculus. We find the top of the hill by using the partial derivatives with regard to μ and σ² - which is generally called the score function (U). Solving the score equations mean that we find which combination of μ and σ² leads to both partial derivates being zero.

Mean

For more challenging models, we often need to use some optimization algorithm. Basically, we let the computer iteratively climb towards the top of the hill. You can use the controls below to see how a gradient ascent or Newton-Raphson algorithm finds its way to the maximum likelihood estimate.

Algorithm

Iterations: 0

Variance

Tip: You can move the values around by dragging them.

Inference

After we've found the MLEs we usually want to make some inferences, so let's focus on three common hypothesis tests. Use the sliders below to change the null hypothesis and the sample size.

Illustration

Sample Size (n)

Null (μ0)

The score function evaluated at the null is,

$U(\mu_0, \hat\sigma_0^2) = \frac{\partial}{\partial \mu_0}\ell(\mu_0, \hat\sigma_0^2) = -Infinity$

The observed Fisher information is the negative of the second derivative. This is related to the curvature of the likelihood function -- try increasing the sample size and note that the peak gets narrower around the MLE and that the information increases. The inverse of I is also the variance of the MLE.

$I(\mu_0, \hat\sigma_0^2) = \frac{\partial^2}{\partial \mu_0^2}\ell(\mu_0, \hat\sigma_0^2) = Infinity$

Hypothesis Tests

We have the following null and alternative hypothesis,

$H_0: \mu = 80 \quad \text{versus} \quad H_1: \mu \ne 80$

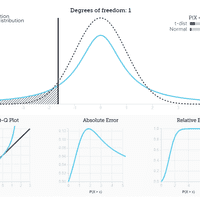
The likelihood ratio test compares the likelihood ratios of two models. In this example it's the likelihood evaluated at the MLE and at the null. This is illustrated in the plot by the vertical distance between the two horizontal lines. If we multiply the difference in log-likelihood by -2 we get the statistic,

$\begin{aligned} \text{LR} &= -2[\ell(\mu_{0}, \hat\sigma^2_{0}) - [\ell(\hat\mu, \hat\sigma^2)]\\ &= NaN \end{aligned}$

Asymptotically LR follows a $\chi^2$ distribution with 1 degrees of freedom, which gives p = NaN.

Note: The figure is simplified and does not account for the fact that each likelihood is based on different variance estimates.

Written by Kristoffer Magnusson, a researcher in clinical psychology. You should follow him on Twitter and come hang out on the open science discord Git Gud Science.

FAQ

What are the formulas?

This page is still under construction, formulas will be added later. Pull requests are welcome!

How do I cite this page?

Cite this page according to your favorite style guide. The references below are automatically generated and contain the correct information.

APA 7

Magnusson, K. (2020). Understanding Maximum Likelihood: An interactive visualization (Version 0.1.2) [Web App]. R Psychologist. https://rpsychologist.com/likelihood/

BibTex

I found a bug/error/typo or want to make a suggestion!

Please report errors or suggestions by opening an issue on GitHub, if you want to ask a question use GitHub discussions

I'm gonna ask a large number of students to visit this site. Will it crash your server?

No, it will be fine. The app runs in your browser so the server only needs to serve the files.

Can I include this visualization in my book/article/etc?

Yes, go ahead! The design of the visualizations on this page is dedicated to the public domain, which means “you can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission” (see Creative common’s CC0-license). Although, attribution is not required it is always appreciated!.

Contribute/Donate

There are many ways to contribute to free and open software. If you like my work and want to support it you can:

Buy Me a Coffee ☕

(or use PayPal)

A huge thanks to the 152 supporters who've bought me a 361 coffees!

Jason Rinaldo bought ☕☕☕☕☕☕☕☕☕☕ (10) coffees

I've been looking for applets that show this for YEARS, for demonstrations for classes. Thank you so much! Students do not need to tolarate my whiteboard scrawl now. I'm sure they'd appreciate you, too.l

JDMM bought ☕☕☕☕☕ (5) coffees

You finally helped me understand correlation! Many, many thanks... 😄

@VicCazares bought ☕☕☕☕☕ (5) coffees

Good stuff! It's been so helpful for teaching a Psych Stats class. Cheers!

Dustin M. Burt bought ☕☕☕☕☕ (5) coffees

Excellent and informative visualizations!

Someone bought ☕☕☕☕☕ (5) coffees

@metzpsych bought ☕☕☕☕☕ (5) coffees

Always the clearest, loveliest simulations for complex concepts. Amazing resource for teaching intro stats!

Ryo bought ☕☕☕☕☕ (5) coffees

For a couple years now I've been wanting to create visualizations like these as a way to commit these foundational concepts to memory. But after finding your website I'm both relieved that I don't have to do that now and pissed off that I couldn't create anything half as beautiful and informative as you have done here. Wonderful job.

Diarmuid Harvey bought ☕☕☕☕☕ (5) coffees

You have an extremely useful site with very accessible content that I have been using to introduce colleagues and students to some of the core concepts of statistics. Keep up the good work, and thanks!

Michael Hansen bought ☕☕☕☕☕ (5) coffees

Keep up the good work!

Michael Villanueva bought ☕☕☕☕☕ (5) coffees

I wish I could learn more from you about stats and math -- you use language in places that I do not understand. Cohen's D visualizations opened my understanding. Thank you

Someone bought ☕☕☕☕☕ (5) coffees

Thank you, Kristoffer

Pål from Norway bought ☕☕☕☕☕ (5) coffees

Great webpage, I use it to illustrate several issues when I have a lecture in research methods. Thanks, it is really helpful for the students:)

@MAgrochao bought ☕☕☕☕☕ (5) coffees

Joseph Bulbulia bought ☕☕☕☕☕ (5) coffees

Hard to overstate the importance of this work Kristoffer. Grateful for all you are doing.

@TDmyersMT bought ☕☕☕☕☕ (5) coffees

Some really useful simulations, great teaching resources.

@lakens bought ☕☕☕☕☕ (5) coffees

Thanks for fixing the bug yesterday!

@LinneaGandhi bought ☕☕☕☕☕ (5) coffees

This is awesome! Thank you for creating these. Definitely using for my students, and me! :-)

@ICH8412 bought ☕☕☕☕☕ (5) coffees

very useful for my students I guess

@KelvinEJones bought ☕☕☕☕☕ (5) coffees

Preparing my Master's student for final oral exam and stumbled on your site. We are discussing in lab meeting today. Coffee for everyone.

Someone bought ☕☕☕☕☕ (5) coffees

What a great site

@Daniel_Brad4d bought ☕☕☕☕☕ (5) coffees

Wonderful work!

David Loschelder bought ☕☕☕☕☕ (5) coffees

Terrific work. So very helpful. Thank you very much.

@neilmeigh bought ☕☕☕☕☕ (5) coffees

I am so grateful for your page and can't thank you enough!

@giladfeldman bought ☕☕☕☕☕ (5) coffees

Wonderful work, I use it every semester and it really helps the students (and me) understand things better. Keep going strong.

Dean Norris bought ☕☕☕☕☕ (5) coffees

Sal bought ☕☕☕☕☕ (5) coffees

Really super useful, especially for teaching. Thanks for this!

dde@paxis.org bought ☕☕☕☕☕ (5) coffees

Very helpful to helping teach teachers about the effects of the Good Behavior Game

@akreutzer82 bought ☕☕☕☕☕ (5) coffees

Amazing visualizations! Thank you!

@rdh_CLE bought ☕☕☕☕☕ (5) coffees

So good!

Amanda Sharples bought ☕☕☕ (3) coffees

Soyol bought ☕☕☕ (3) coffees

Someone bought ☕☕☕ (3) coffees

Kenneth Nilsson bought ☕☕☕ (3) coffees

Keep up the splendid work!

@jeremywilmer bought ☕☕☕ (3) coffees

Love this website; use it all the time in my teaching and research.

Someone bought ☕☕☕ (3) coffees

Powerlmm was really helpful, and I appreciate your time in putting such an amazing resource together!

DR AMANDA C DE C WILLIAMS bought ☕☕☕ (3) coffees

This is very helpful, for my work and for teaching and supervising

Georgios Halkias bought ☕☕☕ (3) coffees

Regina bought ☕☕☕ (3) coffees

Love your visualizations!

Susan Evans bought ☕☕☕ (3) coffees

Thanks. I really love the simplicity of your sliders. Thanks!!

@MichaMarie8 bought ☕☕☕ (3) coffees

Thanks for making this Interpreting Correlations: Interactive Visualizations site - it's definitely a great help for this psych student! 😃

Zakaria Giunashvili, from Georgia bought ☕☕☕ (3) coffees

brilliant simulations that can be effectively used in training

Someone bought ☕☕☕ (3) coffees

@PhysioSven bought ☕☕☕ (3) coffees

Amazing illustrations, there is not enough coffee in the world for enthusiasts like you! Thanks!

Cheryl@CurtinUniAus bought ☕☕☕ (3) coffees

🌟What a great contribution - thanks Kristoffer!

vanessa moran bought ☕☕☕ (3) coffees

Wow - your website is fantastic, thank you for making it.

Someone bought ☕☕☕ (3) coffees

mikhail.saltychev@gmail.com bought ☕☕☕ (3) coffees

Thank you Kristoffer This is a nice site, which I have been used for a while. Best Prof. Mikhail Saltychev (Turku University, Finland)

Someone bought ☕☕☕ (3) coffees

Ruslan Klymentiev bought ☕☕☕ (3) coffees

@lkizbok bought ☕☕☕ (3) coffees

Keep up the nice work, thank you!

@TELLlab bought ☕☕☕ (3) coffees

Thanks - this will help me to teach tomorrow!

SCCT/Psychology bought ☕☕☕ (3) coffees

Keep the visualizations coming!

@elena_bolt bought ☕☕☕ (3) coffees

Thank you so much for your work, Kristoffer. I use your visualizations to explain concepts to my tutoring students and they are a huge help.

A random user bought ☕☕☕ (3) coffees

Thank you for making such useful and pretty tools. It not only helped me understand more about power, effect size, etc, but also made my quanti-method class more engaging and interesting. Thank you and wish you a great 2021!

@hertzpodcast bought ☕☕☕ (3) coffees

We've mentioned your work a few times on our podcast and we recently sent a poster to a listener as prize so we wanted to buy you a few coffees. Thanks for the great work that you do!Dan Quintana and James Heathers - Co-hosts of Everything Hertz

Cameron Proctor bought ☕☕☕ (3) coffees

Used your vizualization in class today. Thanks!

eshulman@brocku.ca bought ☕☕☕ (3) coffees

My students love these visualizations and so do I! Thanks for helping me make stats more intuitive.

Someone bought ☕☕☕ (3) coffees

Adrian Helgå Vestøl bought ☕☕☕ (3) coffees

@misteryosupjoo bought ☕☕☕ (3) coffees

For a high school teacher of psychology, I would be lost without your visualizations. The ability to interact and manipulate allows students to get it in a very sticky manner. Thank you!!!

Chi bought ☕☕☕ (3) coffees

You Cohen's d post really helped me explaining the interpretation to people who don't know stats! Thank you!

Someone bought ☕☕☕ (3) coffees

You doing useful work !! thanks !!

@ArtisanalANN bought ☕☕☕ (3) coffees

Enjoy.

@jsholtes bought ☕☕☕ (3) coffees

Teaching stats to civil engineer undergrads (first time teaching for me, first time for most of them too) and grasping for some good explanations of hypothesis testing, power, and CI's. Love these interactive graphics!

@notawful bought ☕☕☕ (3) coffees

Thank you for using your stats and programming gifts in such a useful, generous manner. -Jess

Mateu Servera bought ☕☕☕ (3) coffees

A job that must have cost far more coffees than we can afford you ;-). Thank you.

@cdrawn bought ☕☕☕ (3) coffees

Thank you! Such a great resource for teaching these concepts, especially CI, Power, correlation.

Julia bought ☕☕☕ (3) coffees

Fantastic work with the visualizations!

@felixthoemmes bought ☕☕☕ (3) coffees

@dalejbarr bought ☕☕☕ (3) coffees

Your work is amazing! I use your visualizations often in my teaching. Thank you.

@PsychoMouse bought ☕☕☕ (3) coffees

Excellent! Well done! SOOOO Useful!😊 🐭

Dan Sanes bought ☕☕ (2) coffees

this is a superb, intuitive teaching tool!

@whlevine bought ☕☕ (2) coffees

Thank you so much for these amazing visualizations. They're a great teaching tool and the allow me to show students things that it would take me weeks or months to program myself.

Someone bought ☕☕ (2) coffees

@notawful bought ☕☕ (2) coffees

Thank you for sharing your visualization skills with the rest of us! I use them frequently when teaching intro stats.

Andrew J O'Neill bought ☕ (1) coffee

Thanks for helping understand stuff!

Someone bought ☕ (1) coffee

Shawn Hemelstrand bought ☕ (1) coffee

Thank you for this great visual. I use it all the time to demonstrate Cohen's d and why mean differences affect it's approximation.

Adele Fowler-Davis bought ☕ (1) coffee

Thank you so much for your excellent post on longitudinal models. Keep up the good work!

Stewart bought ☕ (1) coffee

This tool is awesome!

Someone bought ☕ (1) coffee

Aidan Nelson bought ☕ (1) coffee

Such an awesome page, Thank you

Someone bought ☕ (1) coffee

Ellen Kearns bought ☕ (1) coffee

Dr Nazam Hussain bought ☕ (1) coffee

Someone bought ☕ (1) coffee

Eva bought ☕ (1) coffee

I've been learning about power analysis and effect sizes (trying to decide on effect sizes for my planned study to calculate sample size) and your Cohen's d interactive tool is incredibly useful for understanding the implications of different effect sizes!

Someone bought ☕ (1) coffee

Thanks a lot!

Someone bought ☕ (1) coffee

Reena Murmu Nielsen bought ☕ (1) coffee

Tony Andrea bought ☕ (1) coffee

Thanks mate

Tzao bought ☕ (1) coffee

Thank you, this really helps as I am a stats idiot :)

Melanie Pflaum bought ☕ (1) coffee

Sacha Elms bought ☕ (1) coffee

Yihan Xu bought ☕ (1) coffee

Really appreciate your good work!

@stevenleung bought ☕ (1) coffee

Your visualizations really help me understand the math.

Junhan Chen bought ☕ (1) coffee

Someone bought ☕ (1) coffee

Michael Hansen bought ☕ (1) coffee

ALEXANDER VIETHEER bought ☕ (1) coffee

mather bought ☕ (1) coffee

Someone bought ☕ (1) coffee

Bastian Jaeger bought ☕ (1) coffee

Thanks for making the poster designs OA, I just hung two in my office and they look great!

@ValerioVillani bought ☕ (1) coffee

Thanks for your work.

Someone bought ☕ (1) coffee

Great work!

@YashvinSeetahul bought ☕ (1) coffee

Someone bought ☕ (1) coffee

Angela bought ☕ (1) coffee

Thank you for building such excellent ways to convey difficult topics to students!

@inthelabagain bought ☕ (1) coffee

Really wonderful visuals, and such a fantastic and effective teaching tool. So many thanks!

Someone bought ☕ (1) coffee

Yashashree Panda bought ☕ (1) coffee

I really like your work.

Ben bought ☕ (1) coffee

You're awesome. I have students in my intro stats class say, "I get it now," after using your tool. Thanks for making my job easier.

Gabriel Recchia bought ☕ (1) coffee

Incredibly useful tool!

Shiseida Sade Kelly Aponte bought ☕ (1) coffee

Thanks for the assistance for RSCH 8210.

@Benedikt_Hell bought ☕ (1) coffee

Great tools! Thank you very much!

Amalia Alvarez bought ☕ (1) coffee

@noelnguyen16 bought ☕ (1) coffee

Hi Kristoffer, many thanks for making all this great stuff available to the community!

Eran Barzilai bought ☕ (1) coffee

These visualizations are awesome! thank you for creating it

Someone bought ☕ (1) coffee

Chris SG bought ☕ (1) coffee

Very nice.

Gray Church bought ☕ (1) coffee

Thank you for the visualizations. They are fun and informative.

Qamar bought ☕ (1) coffee

Tanya McGhee bought ☕ (1) coffee

@schultemi bought ☕ (1) coffee

Neilo bought ☕ (1) coffee

Really helpful visualisations, thanks!

Someone bought ☕ (1) coffee

This is amazing stuff. Very slick.

Someone bought ☕ (1) coffee

Sarko bought ☕ (1) coffee

Thanks so much for creating this! Really helpful for being able to explain effect size to a clinician I'm doing an analysis for.

@DominikaSlus bought ☕ (1) coffee

Thank you! This page is super useful. I'll spread the word.

Someone bought ☕ (1) coffee

Melinda Rice bought ☕ (1) coffee

Thank you so much for creating these tools! As we face the challenge of teaching statistical concepts online, this is an invaluable resource.

@tmoldwin bought ☕ (1) coffee

Fantastic resource. I think you would be well served to have one page indexing all your visualizations, that would make it more accessible for sharing as a common resource.

Someone bought ☕ (1) coffee

Fantastic Visualizations! Amazing way to to demonstrate how n/power/beta/alpha/effect size are all interrelated - especially for visual learners! Thank you for creating this?

@jackferd bought ☕ (1) coffee

Incredible visualizations and the best power analysis software on R.

Cameron Proctor bought ☕ (1) coffee

Great website!

Someone bought ☕ (1) coffee

Hanah Chapman bought ☕ (1) coffee

Thank you for this work!!

Someone bought ☕ (1) coffee

Jayme bought ☕ (1) coffee

Nice explanation and visual guide of Cohen's d

Bart Comly Boyce bought ☕ (1) coffee

thank you

Dr. Mitchell Earleywine bought ☕ (1) coffee

This site is superb!

Florent bought ☕ (1) coffee

Zampeta bought ☕ (1) coffee

thank you for sharing your work.

Mila bought ☕ (1) coffee

Thank you for the website, made me smile AND smarter :O enjoy your coffee! :)

Deb bought ☕ (1) coffee

Struggling with statistics and your interactive diagram made me smile to see that someone cares enough about us strugglers to make a visual to help us out!😍

Someone bought ☕ (1) coffee

@exerpsysing bought ☕ (1) coffee

Much thanks! Visualizations are key to my learning style!

Someone bought ☕ (1) coffee

Webmentions

0 0

What's this?

Yann de Mey 2022-11-09

I am indeed using your medium guide to bring this into practice in @Stata on Friday ;) I also link to these pages as they nicely add some visual intuition for the students as well: aboveintelligent.com/deep-learning-… and rpsychologist.com/likelihood

Andrew Camp 2022-02-14

@Kate__Barnes @AlisonHeape @SarahR_Morris @gema_zamarro Check this out - rpsychologist.com/likelihood/

𝚌𝚎𝚙𝚝𝚛𝚎𝚎 2021-08-11

たのしいやつだ Understanding Maximum Likelihood An Interactive Visualization rpsychologist.com/likelihood/

Farzana Khatun Tania 2021-05-14

This 👇! I try to illustrate the maximum likelihood method. I've also included the likelihood ratio test, Wald test, and Score test. rpsychologist.com/d3/likelihood/ twitter.com/krstoffr/statu…